LAT Homework
02.10.2009
Consider the automata construction from proof of the Myhill-Nerode theorem for a language L. Prove
- (a) the constructed automaton A is the minimal automaton (in the number of states) that recognizes L;
- (b) any minimal automaton recognizing L is isomorphic to A.
06.11.2009
- Given a reachability game (G,F), give an algorithm that computes the 0-Attractor(F) set in time O(|E|).
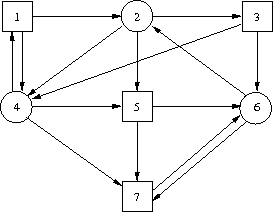
- Consider the game graph shown in below and the following winning conditions: a) Occ(ρ) ∩ {1} ≠ ∅ and b) Occ(ρ) ⊆ {1,2,3,4,5,6} and c) Inf(ρ) ∩ {4,5} ≠ ∅. Compute the winning regions and corresponding winning strategies showing the intermediate steps (i.e., the Attractor and Recurrence sets) of the computation.
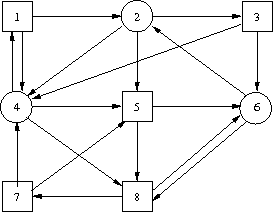
- Given a game graph G=(S,S0,T) and a set F ⊆ S. Let W0 and W_1 be the winning regions of Player 0 and Player 1, respectively, in the Buchi game (G,F). Prove or disprove:
- The winning set of Player 0 in the safety game for (G,W0) is W0,
- If f0 is a winning strategy for Player 0 in the safety game for (G,W0), then f0 is also a winning strategy for Player 0 in the Buchi game for (G,F),
- the winning set of Player 1 in the guaranty game for (G,W_1) is W_1, and
- if f_1 is a winning strategy for Player 1 in the guaranty game for (G,W0), then f_1 is a winning strategy in the Buchi game (G,F).
13.11.2009
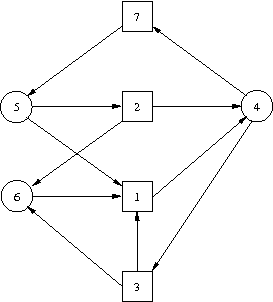
- Consider the game graph shown below. Let the winning condition for Player 0 be Occ(ρ)={1,2,3,4,5,6,7}
- Find the winning region for Player 0 and describe a winning strategy
- A winning strategy is called “uniform” if it is a winning strategy from every winning state in the game. Let (G,p) be a weak parity game and let W0 be the winning region of Player 0. For all s ∈ W0 let f_s be a positional winning strategy from s for Player 0. Construct a uniform winning strategy f from the strategies f_s meaning that for every s ∈ W0 there is a t ∈ W0, s.t. f(s) = f_t(s).
27.11.2009
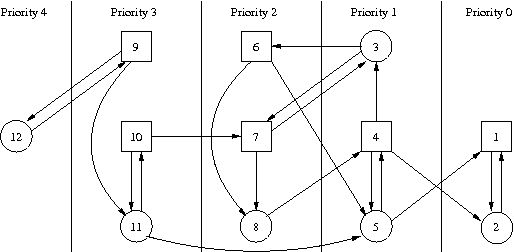
- Consider the game shown on page 6 of slide10.pdf. We propose the following “latest appearance queue” (LAQ) strategy for Player 0, initializing the queue with s1s2s3s4,
- add the current state at the front of the LAQ and delete the last state
- move to the state ti whose number i is the number of different states in the current LAQ,
e.g., for the sequence of states s1, s3, s3, s4, s1,… we obtain the following sequence of LAQs: s1s2s3s4, s1s1s2s3, s3s1s1s2, s3s3s1s1, s4s3s3s1,s1s4s3s3,…
Decide wheater the new LAQ strategy is a winning strategy for Player 0. Prove this or give a counter-example.
- Let A=(S,s0,T,p) be a parity automaton with p:S → {1,..,k}. Construct a Streett automaton B=(S,s0,T,F) equivalent to A that has the same transition structure as A. (i.e., find a suitable set of Streett pairs (F_i,E_i))
6.12.2009
- Exam-like problems on automata and Presburger Arithmetic homework.pdf